【初学者向け】グリーンのひずみテンソルと微小ひずみテンソル

はじめに

本記事ではベクトルと行列のそれぞれを明示するために行列Aの場合は$\left[A\right]$、ベクトルAの場合は$\{A\}$のように[]と{}を使い分けています。また、初学者の脳みそをパンクさせないためにラグランジュ法とオイラー法についての紹介は行っていません。

本記事ではグリーンのひずみテンソルについて簡単な紹介しか行わないため、詳細を知りたい方はこちら↓の参考文献¹などを参照してください²。

この記事を書いた動機

昨年・一昨年と連続体力学（特に固体力学分野）の勉強をする機会があったのですが、主にテンソルの総和規約のせいで、とても難しく感じました。

確かに、ある概念を数学的に無駄のない形で定義通り伝える重要性は理解できますが、非常に厳密な定義や抽象的な説明が初学者の理解度を深めるのに有効であるとは思いません。

これを解決する方法として、少々時間のかかる方法ですが、初学者が従来学習してきた（はずの）応力・ひずみの概念、および行列・ベクトルの様々な計算とテンソルの演算方法を具体的に紐づける必要があると感じました（というよりも私はこれでようやく様々なテンソルの話を理解できるようになりました）。

そこで、本記事では一例としてグリーンのひずみテンソルの定義式に着目し、その定義式に則りつつも、より具体的な行列・ベクトルの計算を介することでこれらの概念を少しでも理解しやすくしたいと思います²。

グリーンのひずみテンソルとは

大変形を意味する有限変形の概念を考える上でも重要なグリーンのひずみテンソルについて、日本機械学会の公式サイトが説明してくれています。

• 機械工学事典 グリーンのひずみテンソル
• 機械工学事典 有限変形

なお、参考文献¹においてグリーンのひずみテンソルは移動前の位置ベクトル$\boldsymbol{\it{A}}, \boldsymbol{\it{B}}$と移動後の位置ベクトル$\boldsymbol{\it{A’}}, \boldsymbol{\it{B’}}$を用いて次の通り定義されています³。

\begin{equation} \boldsymbol{A’}\cdot\boldsymbol{B’}-\boldsymbol{A}\cdot\boldsymbol{B}=\rm{2\it{E_{ij}}\it{A_{i}}\it{B_{j}}}\\\ \end{equation}

定義通り説明するとこの表現が奇麗な表現になります。ただし、初学者がこの式をただ眺めても 「良く分からない行列計算を良く分からない下付き文字（総和規約）を使って表現しているんだなぁ」くらいにしか分からないと思います。

グリーンのひずみテンソルの導出のような何か

まず、下図の様に位置ベクトル$\{A\}$が変位$u, v, w$によってベクトル$\{A’\}$となる場合を考えます⁴。なお、ベクトル$\{A\}$は式(2)で表されるものとしています。

\begin{equation} \{A\}= \begin{Bmatrix}\rm{d}x\\ \rm{d}y\\ \rm{d}z\end{Bmatrix} \end{equation}

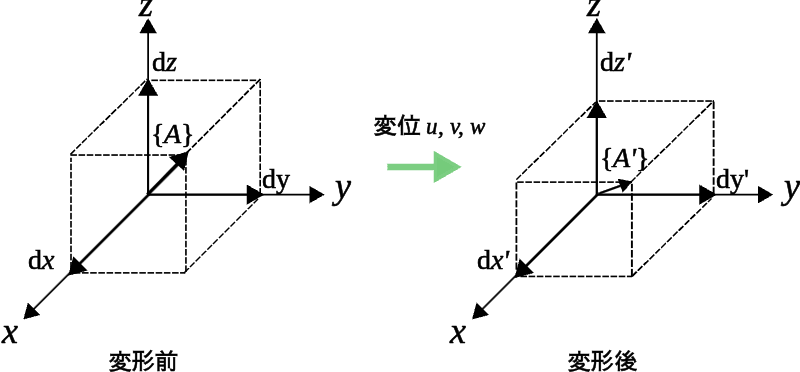
続いて次式を計算します⁵。

\begin{equation} \{A’\}\cdot\{A’\}-\{A\}\cdot\{A\} \end{equation}

なお、計算の際にはベクトル$\{A’\}$が変位勾配テンソル$\left[ \it{F}\rm~\right]$と$\{A\}$を用いて次式で表せることを用います。

\begin{equation} \{A’\}=\{A\}+\left[ \it{F}\rm~\right]\{A\}=\begin{Bmatrix}\rm{d}x\\ \rm{d}y\\ \rm{d}z\end{Bmatrix}+ \begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} & \frac{\partial u}{\partial z} \\\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z} \\\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{bmatrix}\begin{Bmatrix}\rm{d}x\\ \rm{d}y\\ \rm{d}z\end{Bmatrix} \end{equation}

式(3)の第一項を抜き出して計算します。

\begin{eqnarray} \{A’\}\cdot\{A’\} &=& \{A’\}^{\mathrm{ T }}\{A’\}\nonumber\\[ 5pt ] &=& \left(\{A\}^{\mathrm{ T }}+\{A\}^{\mathrm{ T }}\left[ \it{F}\rm~\right]^{\mathrm{ T }}\right)\left(\{A\}+\left[ \it{F}\rm~\right]\{A\}\right)\nonumber\\[ 5pt ] &=& \{A\}\cdot\{A\}+\{A\}^{\mathrm{ T }}\left(\left[ \it{F}\rm~\right]+\left[ \it{F}\rm~\right]^{\mathrm{ T }}+\left[ \it{F}\rm~\right]^{\mathrm{ T }}\left[ \it{F}\rm~\right]\right)\{A\} \end{eqnarray}

式(5)を用いることで式(3)は次の通り変形できます。

\begin{equation} \{A’\}\cdot\{A’\}-\{A\}\cdot\{A\} = \{A\}^{\mathrm{ T }}\left(\left[ \it{F}\rm~\right]+\left[ \it{F}\rm~\right]^{\mathrm{ T }}+\left[ \it{F}\rm~\right]^{\mathrm{ T }}\left[ \it{F}\rm~\right]\right)\{A\} \end{equation}

ここで、式(1)において$\{A\}=\{B\}$とすれば式(6)と同様の式となり、$\{A\}^{\mathrm{ T }}$と$\{A\}$に挟まれた項がグリーンのひずみテンソルを2倍したもの（$2\left[E\right]$）であることが分かります。従って、

\begin{eqnarray} 2\left[E\right]&=&\left[ \it{F}\rm~\right]+\left[ \it{F}\rm~\right]^{\mathrm{ T }}+\left[ \it{F}\rm~\right]^{\mathrm{ T }}\left[ \it{F}\rm~\right]\nonumber\\[ 5pt ] &=& \begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} & \frac{\partial u}{\partial z} \\\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z} \\\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{bmatrix}+ \begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial v}{\partial x} & \frac{\partial w}{\partial x}\\\ \frac{\partial u}{\partial y} & \frac{\partial v}{\partial y} & \frac{\partial w}{\partial y} \\\ \frac{\partial u}{\partial z} & \frac{\partial v}{\partial z} & \frac{\partial w}{\partial z} \end{bmatrix}+ \begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial v}{\partial x} & \frac{\partial w}{\partial x}\\\ \frac{\partial u}{\partial y} & \frac{\partial v}{\partial y} & \frac{\partial w}{\partial y} \\\ \frac{\partial u}{\partial z} & \frac{\partial v}{\partial z} & \frac{\partial w}{\partial z} \end{bmatrix} \begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} & \frac{\partial u}{\partial z} \\\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z} \\\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{bmatrix}\nonumber\\[ 5pt ] &=& \begin{bmatrix} 2\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} & \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x} \\\ \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y} & 2\frac{\partial v}{\partial y} & \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y} \\\ \frac{\partial w}{\partial x}+\frac{\partial v}{\partial z} & \frac{\partial w}{\partial y}+\frac{\partial v}{\partial z} & 2\frac{\partial w}{\partial z} \end{bmatrix}+ \begin{bmatrix} \left(\frac{\partial u}{\partial x}\right)^2+\left(\frac{\partial v}{\partial x}\right)^2+\left(\frac{\partial w}{\partial x}\right)^2 & \frac{\partial u}{\partial x}\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\frac{\partial v}{\partial y}+\frac{\partial w}{\partial x}\frac{\partial w}{\partial y} & \frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial x}\frac{\partial v}{\partial z}+\frac{\partial w}{\partial x}\frac{\partial w}{\partial z} \\\ \frac{\partial u}{\partial y}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial w}{\partial y}\frac{\partial w}{\partial x} &\left(\frac{\partial u}{\partial y}\right)^2+\left(\frac{\partial v}{\partial y}\right)^2+\left(\frac{\partial w}{\partial y}\right)^2 & \frac{\partial u}{\partial y}\frac{\partial u}{\partial z}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\frac{\partial w}{\partial z} \\\ \frac{\partial u}{\partial z}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial z}\frac{\partial v}{\partial x}+\frac{\partial w}{\partial z}\frac{\partial w}{\partial x} & \frac{\partial u}{\partial z}\frac{\partial u}{\partial y}+\frac{\partial v}{\partial z}\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\frac{\partial w}{\partial y} & \left(\frac{\partial u}{\partial z}\right)^2+\left(\frac{\partial v}{\partial z}\right)^2+\left(\frac{\partial w}{\partial z}\right)^2 \end{bmatrix} \end{eqnarray}

そして式(7)の両辺に1/2を掛けて、総和規約を用いてを表すとよく教科書などで見かけるグリーンのひずみテンソルが出てきます⁶$(i, j, p = 1, 2, 3)$。

\begin{equation} E_{ij}=\frac{1}{2}\left(\nabla_{i}u_{j}+\nabla_{j}u_{i}+\nabla_{i}u_{p}\nabla_{j}u_{p}\right) \end{equation}

微小ひずみテンソルの導出

グリーンのひずみテンソルの二次以降の項（非線形項）を無視することで微小ひずみテンソル$[\varepsilon], \varepsilon_{ij}$が得られます。これらをまとめると式(9)となり、総和規約を用いることで式(10)となります。

\begin{eqnarray} [\varepsilon]&=&\frac{1}{2}\begin{bmatrix} 2\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} & \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x} \\\ \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y} & 2\frac{\partial v}{\partial y} & \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y} \\\ \frac{\partial w}{\partial x}+\frac{\partial v}{\partial z} & \frac{\partial w}{\partial y}+\frac{\partial v}{\partial z} & 2\frac{\partial w}{\partial z} \end{bmatrix}\\[ 5pt ] \varepsilon_{ij}&=&\frac{1}{2}\left(\nabla_{i}u_{j}+\nabla_{j}u_{i}\right) \end{eqnarray}

したがって、微小ひずみテンソルの各成分は工学ひずみの垂直ひずみと1/2倍されたせん断ひずみから構成されていることが分かります。

追記（2022/1/2）

上記と似た方法でグリーンのひずみテンソル（とアルマンシのひずみテンソル）について説明している資料があったので紹介しておきます。

• 材料力学を楽しむ会 2019年度 第1回

こちらの資料↑では本記事で扱わなかった、ラグランジュ法とオイラー法による表現・アルマンシのひずみテンソルの二点についても触れています。初学者には難しいかもしれませんが、比較的読みやすい資料だと思います。また、こちらの記事では、本記事で扱った$\{A\}$と$\{A’\}$が$\rm{d}\it{p}$と$\rm{d}\boldsymbol{P}$に対応しています。

まとめ

私の場合、今回説明してきたような具体的な行列計算を通してようやくひずみテンソルの概念を理解できました。それと同時に、総和規約用いた計算の便利さ・計算量の少なさも理解することが出来ました。

もし仮に教える側に回ることがあったら、（どうしても時間は掛かりますが）一度は今回のような行列計算を行うことをおすすめしつつ、ある程度慣れてきたところで総和規約を使い始めるかなあと思います。

ちなみにですが、今回紹介したのはあくまでも各テンソルの概念を理解するために必要最低限の説明しかしていません。これらのテンソルには他にも様々な幾つかの面白い性質があるので、気になったらぜひ色々な文献をあさってみてください。