ベルヌーイ・オイラー梁とティモシェンコはりの違いの比較（理論編）

はじめに

つい最近ティモシェンコのはり理論について学習する機会があったのですが、あまり簡易に説明されたものが無かったので自分で書くことにしました。完全に理解するためにベルヌーイ・オイラー梁の理論との比較を行います。

なお、本記事では一部の式の導出を省略していますので詳細については以下の文献などを参照してください。

追記

具体的な計算例として↓のページで両者の方法を用いて梁の固有角振動数を求めてみました。理論だけでなく計算例も見たい方は参照してみてください。

ティモシェンコのはり理論とは

学部生レベルの材料力学で扱うようなベルヌーイ・オイラー梁の理論とは異なり、ティモシェンコのはり理論は梁に作用するせん断力を考慮して梁の変位を計算する理論です。正確な定義はこちらにある通りです。

なお、ティモシェンコのはり理論を用いて梁の振動を考えるときには曲げモーメントによる回転運動に対する回転慣性を考慮する必要があり、これもベルヌーイ・オイラー梁の理論と異なる部分でもあります。

それぞれの理論での横振動方程式

下図のような梁の微小要素に対してベルヌーイ・オイラー梁とティモシェンコはりのそれぞれの理論を用いて梁の横振動方程式を考えます。なお、簡単のため梁は均質で一様な断面をもつと仮定します。

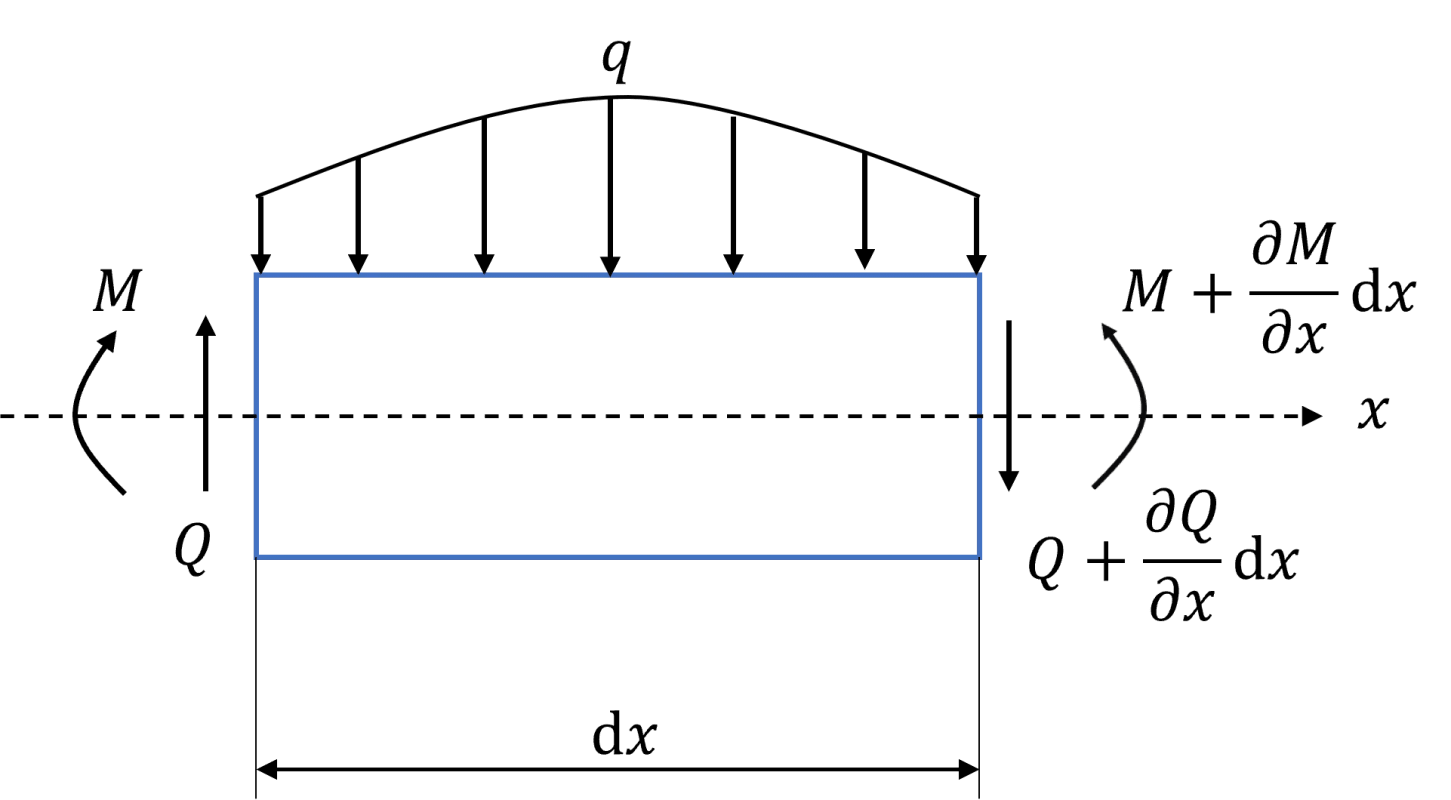
なお、式変形で用いる変数はそれぞれ以下の物理量を指しています。

記号	説明	記号	説明
$Q(x, t)$	せん断力	$M(x, t)$	曲げモーメント
$q(x, t)$	単位長さ当たりの任意の分布荷重	$dx$	$x$軸方向の微小長さ
$E$	ヤング率	$\nu$	ポアソン比
$G$	横弾性係数	$\rho$	密度
$A$	断面積
$\theta (x, t)$	たわみ角	$w(x, t)$	たわみ

ベルヌーイ・オイラー梁の場合

ベルヌーイ・オイラー梁は、一般的に材料力学で扱う梁の変形に関する理論を指しており、その名の通りベルヌーイ・オイラーの仮定が用いられています。

この理論は比較的簡単なので説明を一部省略します。途中式の導出など、詳しい説明は文献¹などを参照してください。

まず微小要素の運動方程式は、

\begin{equation} \rho Adx\frac{\partial^2w}{\partial t^2}=\frac{\partial Q}{\partial x}dx+qdx \end{equation}

と表せます。ここで、

\begin{equation} Q=\frac{\partial M}{\partial x},\ M=-EI\frac{\partial\theta}{\partial x},\ \theta=\frac{\partial w}{\partial x} \end{equation}

の関係を用いて式(1)を変形します。

\begin{eqnarray} \rho A\frac{\partial^2w}{\partial t^2}&=&\frac{\partial}{\partial x}\left(\frac{\partial M}{\partial x}\right)+q\nonumber\\ &=&\frac{\partial^2}{\partial x^2}\left(-EI\frac{\partial\theta}{\partial x}\right)+q=-EI\frac{\partial^3}{\partial x^3}\left(\frac{\partial w}{\partial x}\right)+q\\ \end{eqnarray}

これをまとめると最終的に横振動方程式は

\begin{equation} \frac{\rho A}{EI}\frac{\partial^2w}{\partial t^2}+\frac{\partial^4w}{\partial x^4}=\frac{q}{EI} \end{equation}

となります²。

ティモシェンコのはり理論の場合

ティモシェンコはりの横振動方程式を導出する際には、せん断変形がどのようなものかを理解しておくことが重要です。せん断変形するはりの様子を下に示します。

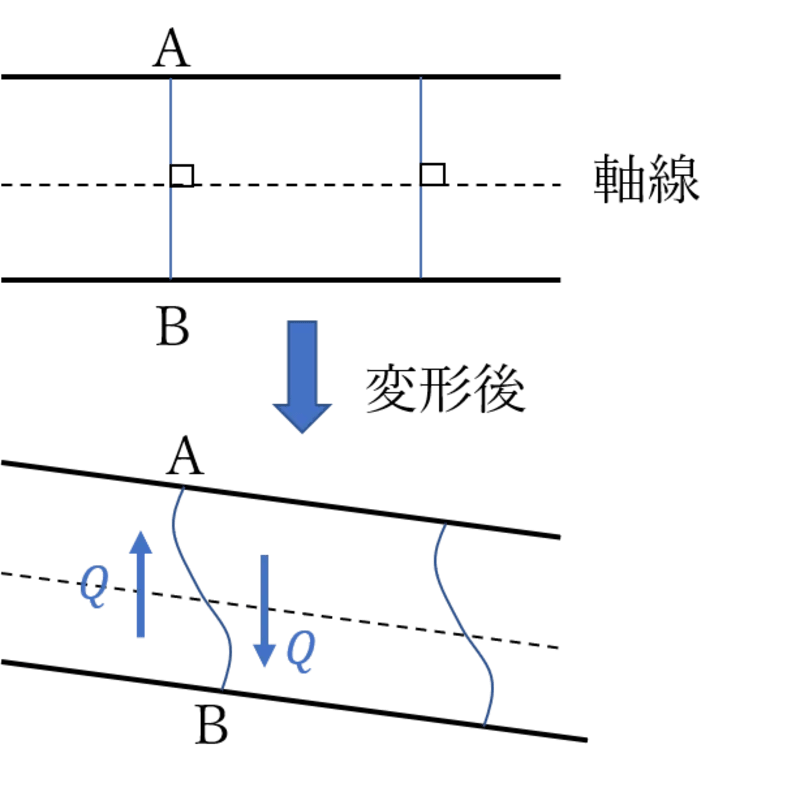
なぜこのように変形するかは、この線分ABの変形をより微小の要素に区切って考えると分かり易いと思います。

線分ABを高さ$dy$の微小な要素に区切って考えると、それぞれの要素はせん断力$\tau$によってせん断変形します。一方、点Aと点Bの付近での変形はほとんどないため、結果として線分ABはうねうねした変形の仕方になります。

なぜこのように変形するかは下記ページなども併せて読んでみると分かりやすいかもしれません。

このようなせん断変形を踏まえ、ティモシェンコのはり理論での横振動方程式の導出方法は次の通りとなります。

1. 非線形に分布するせん断ひずみを一様分布のせん断ひずみに変換
2. 微小体積での運動方程式を導出
3. 回転慣性を考慮してモーメントのつり合い式を導出
4. 運動方程式、曲げモーメントの式およびモーメントのつり合い式から横振動方程式を導出

また、新たに以下の変数を定義し、

変数	説明	変数	説明
$\theta_0$, $w_0$	せん断力によるたわみ角とたわみ	$\theta_1$, $w_1$	曲げモーメントによるたわみ角とたわみ
$I$	断面二次モーメント	$\kappa$	せん断変形の形状係数
$\gamma_0$	せん断変形によるひずみまたはたわみ角

曲げモーメント$M$について次の仮定²を適応します。

たわみ曲線が時間的に変化する場合にも，曲げモーメントと曲率半径との関係は静荷重を受けた場合と同じである．従って、

\begin{equation} M=-EI\frac{\partial\theta_1}{\partial x} \end{equation}

【非線形に分布するせん断ひずみを一様分布のせん断ひずみに変換】

本来、非一様に分布しているせん断ひずみを一様分布のひずみであると近似します。具体的には、本来下図左側の様にせん断変形した断面を、右側のように簡単化します。

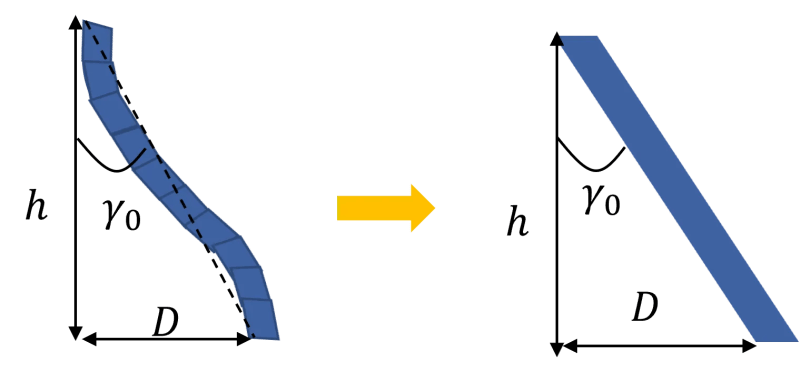
この際、せん断変形の形状係数$\kappa$が得られます。$\kappa$の導出についてはこちらを参照してください。$\kappa$は具体的には以下の式で表せます³。

\begin{equation} \kappa=\frac{\gamma_0AG}{Q} \end{equation}

【微小体積での運動方程式を導出】

ティモシェンコはりの場合の運動方程式は式(1)と同じです。したがって、

\begin{equation} \rho Adx\frac{\partial^2w}{\partial t^2}=\frac{\partial Q}{\partial x}dx+qdx\nonumber \end{equation}

です。

【回転慣性を考慮してモーメントのつり合い式を導出】

モーメントのつり合い式を考える際には、曲げモーメントによる回転運動に対する回転慣性を考慮する必要があります。

ここで当然、「せん断力によって回転運動しないのか…？」という疑問が出ると思いますが、微小要素の回転運動は曲げモーメント$M$によってのみ生じます。

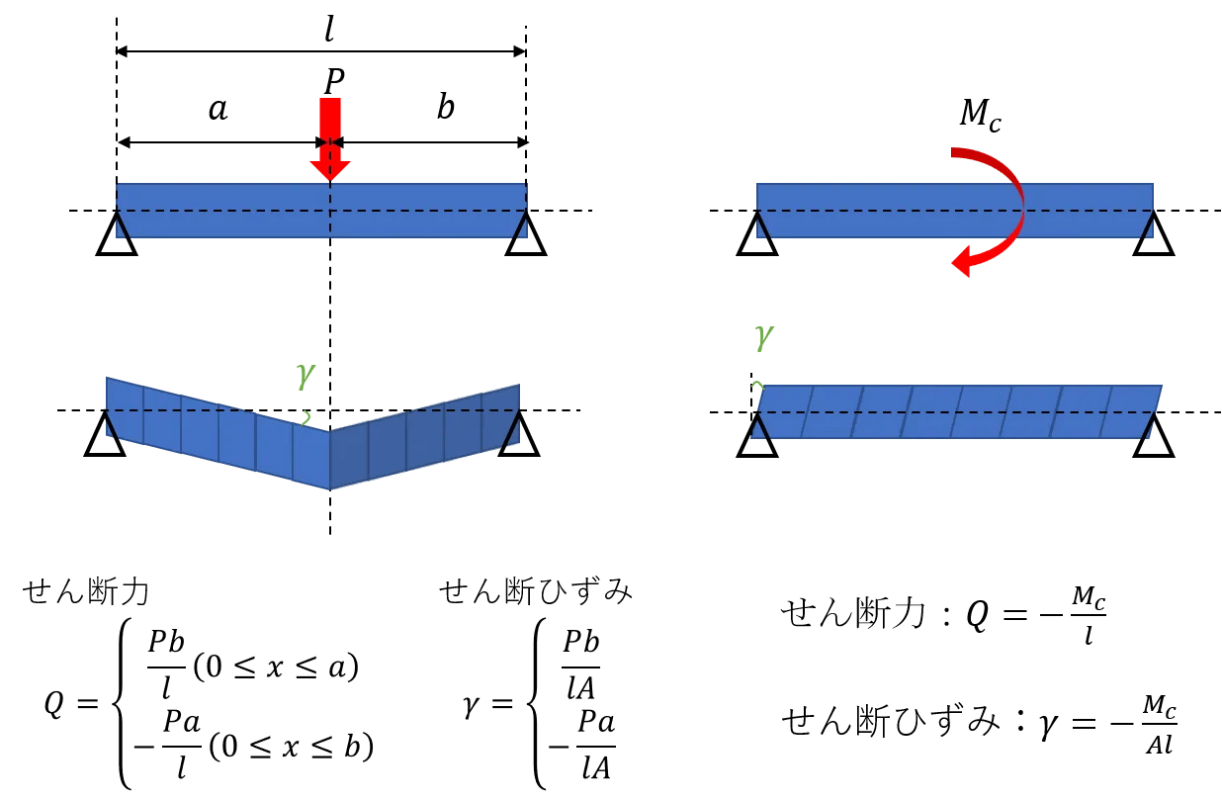
例えば、下記のような梁に集中荷重や曲げモーメントが作用している場合を考えてみましょう。この場合、せん断力$Q$とせん断ひずみ$\gamma$はそれぞれ図中に示した通りとなり、せん断力によって梁の各要素が変形はしますが、回転運動はしません⁴。

以上を踏まえ、慣性モーメントと断面二次モーメントの関係を用いてモーメントのつり合い式を導出すると、

\begin{equation} \frac{\partial M}{\partial x}dx-2Q\frac{dx}{2}-\frac{\partial Q}{\partial x}dx\frac{dx}{2}+\rho Idx\frac{\partial^2\theta_1}{\partial t^2}=0 \end{equation}

となります。上述の通り、せん断力によって回転運動は生じないので、回転慣性の項は$\theta_1$のみで表すことができます。なお、梁の微小要素に作用する分布荷重$q(x, t)$によるモーメントは無視できるとしています。

式(7)の左辺第3項は他の項と比べて微小なのでそれを無視し整理すると、モーメントのつり合い式は

\begin{equation} Q=\frac{\partial M}{\partial x}+\rho I\frac{\partial^2\theta_1}{\partial t^2} \end{equation}

となります²。

【運動方程式、曲げモーメントの式およびモーメントのつり合い式から横振動方程式を導出】

はりの微小要素の変形について、せん断力によるたわみ角$\theta_0$は形状係数$\kappa$を用いて

\begin{equation} \theta_0=\frac{\partial w_0}{\partial x}=\frac{\kappa Q}{AG} \end{equation}

と表せ²、（曲げモーメントによるたわみ角）=（全体のたわみ角）-（せん断力によるたわみ角）なので、

\begin{equation} \theta_1=\frac{\partial w}{\partial x}-\theta_0=\frac{\partial w}{\partial x}-\frac{\kappa Q}{AG} \end{equation}

が成り立ちます²。式(8)と式(10)から、モーメントのつり合い式をたわにを用いて表すと、

\begin{equation} Q=\frac{\partial M}{\partial x}+\rho I\frac{\partial^2}{\partial t^2}\left(\frac{\partial w}{\partial x}-\frac{\kappa Q}{AG}\right)=\frac{\partial M}{\partial x}+\rho I\left(\frac{\partial^3w}{\partial x\partial t^2}-\frac{\kappa}{AG}\frac{\partial^2Q}{\partial t^2}\right) \end{equation}

となります。また、式(1)と式(11)から、運動方程式をたわみを用いて表すと、

\begin{equation} \rho A\frac{\partial^2w}{\partial t^2}=\frac{\partial}{\partial x}\left\{\frac{\partial M}{\partial x}+\rho I\left(\frac{\partial^3w}{\partial x\partial t^2}-\frac{\kappa}{AG}\frac{\partial^2Q}{\partial t^2}\right)\right\}+q \end{equation}

となります。式(5), (10)より、

\begin{equation} M=-EI\frac{\partial\theta_1}{\partial x}=-EI\left(\frac{\partial^2w}{\partial x^2}-\frac{\kappa}{AG}\frac{\partial Q}{\partial x}\right) \end{equation}

となり、式(1)より、

\begin{equation} \frac{\partial Q}{\partial x}=\rho A\frac{\partial^2w}{\partial t^2}-q \end{equation}

であるので、式(13), (14)より次の式を導けます。

\begin{equation} M=-EI\left(\frac{\partial^2w}{\partial x^2}-\frac{\rho\kappa}{G}\frac{\partial^2w}{\partial t^2}-\frac{\kappa}{AG}q\right) \end{equation}

式(12), (15)より、

\begin{equation} \rho A\frac{\partial^2w}{\partial t^2}=-EI\left(\frac{\partial^4w}{\partial x^4}-\frac{\rho\kappa}{G}\frac{\partial^4w}{\partial t^2\partial x^2}-\frac{\kappa}{AG}\frac{\partial^2q}{\partial x^2}\right)+\rho I\left(\frac{\partial^4w}{\partial x^2\partial t^2}-\frac{\kappa}{AG}\frac{\partial^3Q}{\partial x\partial t^2}\right)+q \end{equation}

となります。また、式(14)から、

\begin{equation} \frac{\partial^3Q}{\partial x\partial t^2}=\rho A\frac{\partial^4w}{\partial t^4}-\frac{\partial^2q}{\partial t^2} \end{equation}

が得られ、これを式(16)へ代入し整理して、

\begin{equation} \frac{\partial^4w}{\partial x^4}+\frac{\rho^2\kappa}{GE}\frac{\partial^4w}{\partial t^4}-\frac{\rho}{E}\left(1+\frac{\kappa E}{G}\right)\frac{\partial^4w}{\partial x^2\partial t^2}+\frac{\rho A}{EI}\frac{\partial^2w}{\partial t^2}=\frac{\kappa}{AG}\frac{\partial^2q}{\partial x^2}-\frac{\kappa\rho}{EAG}\frac{\partial^2q}{\partial t^2}+\frac{q}{EI} \end{equation}

となります。なお、右辺の分布荷重$q(x, t)$は任意であるため、改めて

\begin{equation} \frac{\kappa}{AG}\frac{\partial^2q}{\partial x^2}-\frac{\kappa\rho}{EAG}\frac{\partial^2q}{\partial t^2}+\frac{q}{EI}=\frac{q\prime}{EI}\nonumber \end{equation}

とおけば、ティモシェンコのはり理論での横振動方程式は次の通りとなります²。

\begin{equation} \frac{\partial^4w}{\partial x^4}+\frac{\rho^2\kappa}{GE}\frac{\partial^4w}{\partial t^4}-\frac{\rho}{E}\left(1+\frac{\kappa E}{G}\right)\frac{\partial^4w}{\partial x^2\partial t^2}+\frac{\rho A}{EI}\frac{\partial^2w}{\partial t^2}=\frac{q\prime}{EI} \end{equation}

式展開がちょっと長くなりましたが、ベルヌーイ・オイラー梁（式(4)）とティモシェンコはり（式(19)）の両者で横振動方程式がこれだけ異なります。

まとめ

ティモシェンコのはり理論ではせん断変形を考えることで、オイラー・ベルヌーイの仮定の一部が当てはまらなくなります。また、振動解析のような動力学を考える際には回転慣性の扱いについて少し注意が必要です。

今回紹介した理論の両者でどれだけ振動数が変わるのか、適当な境界条件を当てはめて試してみても面白そう（やるかどうかは未定）。