ベルヌーイ・オイラー梁とティモシェンコはりの違いの比較（計算編）

Jun 14, 2022
Sep 23, 2023
Math

はじめに

この記事は前回の記事の続きで、ベルヌーイ・オイラー梁とティモシェンコはりの違いを実際に計算を通して調べてみようという趣旨の記事です。前回の記事はこちらです。

なお、この記事では一部説明を省略している部分もあるので、詳しくは以下の文献などを参照してください。

注意

前回の記事では梁に任意の分布荷重$q(x, t)$が作用している場合を考えましたが、 ~~これを解くのは面倒なので~~ 本記事の趣旨は二つの理論の単純な比較なので、以降、$q(x, t)=0$つまり自由振動の場合を考えます。

なお、$q(x, t)\ne0$とした強制振動の場合の解析方法は文献¹に記載されています。

梁についての条件

梁は下図の様に両端単純支持されたものを考えます。

beam

ベルヌーイ・オイラー梁の場合

前回の記事から、ベルヌーイ・オイラー梁の横振動方程式は次の通り表せます。

\begin{equation} \frac{\rho A}{EI}\frac{\partial^2w}{\partial t^2}+\frac{\partial^4w}{\partial x^4}=0 \end{equation}

幾つかの解の表し方がありますが、今回は文献[1]¹に記載された方法に従います。まず式(1)を見て分かる通り変数分離型で解けるので、変位$w(x, t)$を

\begin{equation} w = W(x)T(t) \end{equation}

と仮定します。これにより、式(1)は

\begin{equation} -\frac{1}{T}\frac{\partial^2T}{\partial t^2}= \frac{EI}{\rho AW}\frac{\partial^4 W}{\partial x^4} \end{equation}

となります。式(3)の両辺が等しくなるためには式(3)の両辺が一定値となる必要があるので、この一定値を$C^2$とおき、

\begin{equation} \frac{\partial^2T}{\partial t^2} + C^2T = 0, \hspace{10pt} EI\frac{\partial^4 W}{\partial x^4} - C^2\rho AW = 0 \end{equation}

となります。ここで、$T=e^{\lambda t}$とおいて式(4)の第一式に代入すると、

\begin{equation} \lambda^2 e^{\lambda t} = -C^2 e^{\lambda t} \therefore \lambda = \pm iC \end{equation}

となります。したがって、式(4)の第一式の一般解は、定数$A’, B’, A, B$を用いて

\begin{equation} T = A’ e^{iCt} + B e^{-iCt}\nonumber\\ \therefore T = A \cos{Ct} + B \sin{Ct} \end{equation}

となります。なお、$A = A’ + B’, \ B = i(A’ - B’)$なので虚数$i$を含んでいますが、最終的に境界条件によって$A, B$が決まるのであまり気にしなくても問題ありません。

式(4)の第二式について、$k^4=\rho A C^2/EI$を導入し、

\begin{equation} \frac{\partial^4 W}{\partial x^4} - k^4 W = 0 \end{equation}

とします。また、$W=e^{\lambda x}$とおくことで、

\begin{equation} \lambda^4 = k^4 \therefore \lambda = \pm k, \ \pm ik \end{equation}

となります。したがって、式(4)の第二式の一般解は

\begin{eqnarray} W &=& C_1 e^{kx} + C_2 e^{-kx} + C_3 e^{ikx} + C_4 e^{-ikx}\nonumber \\ &=& C_1 (\cosh{kx}+\sinh{kx}) + C_2(\cosh{kx}-\sinh{kx}) + C*{3}’ \cos{kx} + C*{4}’ \sin{kx}\nonumber \\ &=& C*{1}’ \cosh{kx} + C*{2}’ \sinh{kx} + C*{3}’ \cos{kx} + C_{4}’ \sin{kx} \end{eqnarray}

と表せます。

境界条件と振動数方程式

式(8)を使って振動数方程式を求めるのですが、境界条件は両端単純支持としています。したがって条件式は

\begin{equation} W(0)=0, {\quad} \frac{\partial^2 W}{\partial x^2}(0)=0, {\quad} W(l)=0, {\quad} \frac{\partial^2 W}{\partial x^2}(l)=0 \end{equation}

となります¹。これにより、次の4つの式が得られます。

\begin{equation} \left. \begin{array}{ll} C’_1+C’_3=0, {\quad} C’_1-C’_3=0\\ C’_2\sinh{kl}+C’_4\sin{kl}=0, {\quad} C’_2\sinh{kl}-C’_4\sin{kl}=0 \end{array} \right\} \end{equation}

上式を行列とベクトルを用いて表すと

\begin{equation} \begin{bmatrix} \sinh{kl} & \sin{kl} \\ \sinh{kl} & -\sin{kl} \end{bmatrix} \left\{ \begin{array}{cc} C’_2\\ C’_4 \end{array} \right\}= \left\{ \begin{array}{cc} 0 \\ 0 \end{array} \right\} \end{equation}

となります。式(11)の$C’_2, C’_4$が共に0以外の解をもつためには、左辺の行列が逆行列をもたないという条件が必要です。したがって、

\begin{equation} \begin{vmatrix} \sinh{kl} & \sin{kl} \\ \sinh{kl} & -\sin{kl} \end{vmatrix}=0 \end{equation}

となります。これを整理すると振動数方程式が得られ、

\begin{equation} \sin{kl}\sinh{kl}=0 \end{equation}

となりますが、

\begin{equation} \sinh{kl} = \frac{e^{kl}+e^{-kl}}{2} >0 \end{equation}

なので、結局、振動数方程式は次式となります¹。

\begin{equation} \sin{kl} = 0 \end{equation}

固有角振動数と固有モード関数

式(15)において$l$は梁の長さであり、具体的に固有角振動数を計算する際に決める値なので、式(15)を$k$について解くと、

\begin{equation} k_n=\frac{n\pi}{l} {\qquad}(n=1, 2, \cdots) \end{equation}

となります¹。ここで、$k^4=\rho A C^2/EI$としていたことを思い出すと、固有角振動数$C_n(>0)$は

\begin{equation} C_n=\left(\frac{n\pi}{l}\right)^2\sqrt{\frac{EI}{\rho A}} {\qquad}(n=1, 2, \cdots) \end{equation}

となります。また、式(15)を式(10)へ代入すると

\begin{equation} C’_2\sinh{kl}=0 {\quad}\therefore C’_2=0 \end{equation}

が得られ、残された$C_4$は任意の値で良いことになります。したがって簡単のために$C_4=1$とすると、$n$次のモード関数は次式で表されることになります¹。

\begin{equation} W_n(x)=\sin{\frac{n\pi}{l}x}{\qquad}(n=1, 2, \cdots) \end{equation}

ティモシェンコはりの場合

任意の分布荷重$q(x, t)$が作用していないときのティモシェンコはりの横振動方程式は次式で表せます。

\begin{equation} \frac{\partial^4w}{\partial x^4}+\frac{\rho^2\kappa}{GE}\frac{\partial^4w}{\partial t^4}-\frac{\rho}{E}\left(1+\frac{\kappa E}{G}\right)\frac{\partial^4w}{\partial x^2\partial t^2}+\frac{\rho A}{EI}\frac{\partial^2w}{\partial t^2}=0 \end{equation}

ここで、境界条件は先ほどと同様に両端単純支持とし、$n$次の振動モードを次の通り仮定します¹（エネルギー法でも同様の仮定を行ので多分妥当っぽい）。

\begin{equation} w = \sin{\frac{n\pi x}{l}}\cos{\omega_n t} \end{equation}

式(21)を式(20)へ代入します。すると、

\begin{equation} \frac{\rho^2 \kappa}{GE}{\omega_n}^4 - \left\{\frac{\rho}{E}\left(1+\frac{\kappa E}{G}\right)\left(\frac{n\pi}{l}\right)^2 + \frac{\rho A}{EI}\right\}{\omega_n}^2 + \left(\frac{n\pi}{l}\right)^4 = 0 \end{equation}

となります。参考文献¹によると、普通上式の${\omega_n}^4$の項は他の項と比べて小さくなるため無視することができるようです。これにより${\omega_n}$は次式で表すことができます。

\begin{equation} \omega_n = \left(\frac{n\pi}{l}\right)^2\sqrt{\frac{EI}{\rho A}\frac{1}{1+\frac{I}{A}\left(1+\frac{\kappa E}{G}\right)\left(\frac{n\pi}{l}\right)^2}} \end{equation}

この結果を式(17)と比べて分かる通り、ティモシェンコはりの場合の横振動の固有角振動数は、ベルヌーイ・オイラー梁のものよりも必ず小さくなります。

と、ここまでで参考文献の方法に則り固有角振動数を求めてきたわけですが、一応式(22)で${\omega_n}^4$の項を無視しなかった場合の固有角振動数$\omega_n$も求めてみます。式(22)から、

\begin{eqnarray} A &=& \frac{\rho^2 \kappa}{GE}\\ B &=& - \left\{\frac{\rho}{E}\left(1+\frac{\kappa E}{G}\right)\left(\frac{n\pi}{l}\right)^2 + \frac{\rho A}{EI}\right\}\\ C &=& \left(\frac{n\pi}{l}\right)^4 \end{eqnarray}

とおけば、

\begin{equation} \omega_n = \sqrt{\frac{-B \pm \sqrt{B^2 - 4AC}}{2A}} \end{equation}

となります。

計算してみた

ベルヌーイ・オイラー梁の場合の固有角振動数を式(17)で、ティモシェンコはりの場合の固有角振動数を式(23), 式(27)で考えます。

なお、それぞれの式での固有角振動数の記号を$\omega_{bo}, \omega_{app}, \omega_{noApp+}, \omega_{noApp-}$とします。boはそのままベルヌーイ・オイラーで、appとnoappは近似（approximation）した解かどうかを示します。+と-は式(27)のルート内の$\pm$を示しています。

材料は工業用純鉄で、計算のパラメータは以下の通りです²。

ヤング率 $E$(GPa)	横弾性係数 $G$(GPa)	密度 $\rho$ (kg/$\text m^3$)	長さ $l$ (m)	幅 $b$ と厚さ$a$ (m)	形状係数 $\kappa$	モード次数$n$
205	81	$7.9 \times 10^3$	1 ~ 10	1	1.2	1

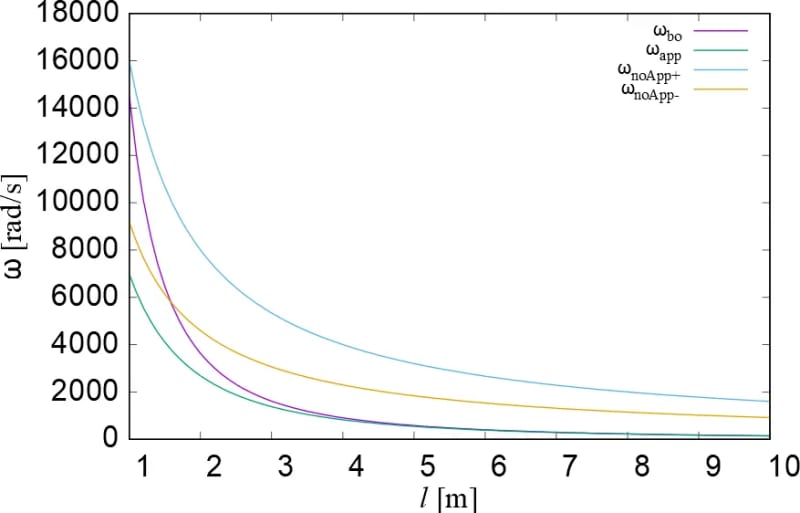
以上の条件で長さ$l$を0.1(m)刻みで変化させた際の固有角振動数を描画してみます。 natural_frequency_graph

上図から、$\omega_{bo}$と、ティモシェンコはりの近似解$\omega_{app}$は大体5[m]程度まではほぼ同じように見えます。一方、ティモシェンコはりについて近似を行わなかった場合の$\omega_{noApp+}$と$\omega_{noApp-}$について、3[m]以降では$\omega_{bo}$と比較的異なる値を取ることが分かりました。

一応 ~~汚いですが~~ プログラムも載せておきます。言語はMATLABです（Octaveでも可）。

clear;

E = 205 * 10^9;
G = 81 * 10^9;
r = 7.9 * 10^3;
l = 1:0.1:10;
h = a = 1;
A = h*a;
k = 1.2;
n = 1;
I = (h^3)*a/12;

o_bo = sqrt(E*I/(r*A)).*(n*pi./l).^2;
o_app = ((n*pi./l).^2).*sqrt((E*I/(r*A)).*(1./(1+(I/A)*(1+k*E/G).*(n*pi./l).^2)));

A1 = (k*r^2)/(G*E)
B1 = -(r/E)*((1+k*E/G).*(n*pi./l).^2 + r*A/(E*I));
C1 = (n*pi./l).^4;

o_noApp1 = sqrt((-B1 + sqrt(B1.^2 -4.*A1.*C1))./(2*A1));
o_noApp2 = sqrt((-B1 - sqrt(B1.^2 -4.*A1.*C1))./(2*A1));

y = [l.' o_bo.' o_app.' o_noApp1.' o_noApp2.'];
y = y.';
fileName = 'omega.dat';
fid = fopen(fileName, 'w');
fprintf(fid, '%f %15.14f %15.14f %15.14f %15.14f\n', y);
fclose(fid);

まとめ

一般にティモシェンコはりとベルヌーイ・オイラー梁の両理論の違いは、梁の長さが短くなればなるほど顕著に表れることが知られています（せん断力の影響を受けるため）。そして今回示したグラフからも同様のことが伺えます。

今回は調べ切れていませんが、以下の点についてはもう少し調べても面白そうですね。

$l$を大きくしたときに、近似しなかった場合の解$\omega_{noApp+}, \omega_{noApp-}$が$\omega_{bo}$と一致するかどうか
両理論での振動モードの違い
（余力があれば）有限要素解析の結果との比較

中川憲治，岩壺卓三，室津義定，”工業振動学　第2版”（1996），森北出版． ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
”理科年表 2020”、丸善出版． ↩︎

Jul 23, 2022
POSTS

Jun 7, 2022
POSTS