オイラーの運動方程式とコーシーの運動方程式【初学者向け】

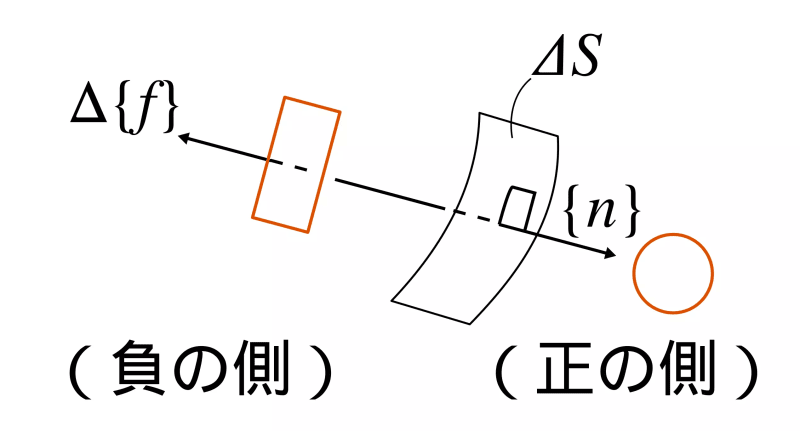
この微小面積要素$\Delta S$の法線ベクトル$\{n\}$が示す方向を正の方向とし、負の方向に働く力を$\Delta \{f\}$としたとき、表面力$\{t\}$は応力ベクトルと呼ばれ、次の通り定義されます¹。 \begin{equation} \{t\}= \lim_{\Delta S \to 0} \frac{\Delta \{f\}}{\Delta S} = \frac{d\{f\}}{ds} \end{equation}

オイラーの第一運動法則

下図の様に物体力と表面力が作用する体積$V$とその内部の微小体積$dV$を考えます。

閉局面

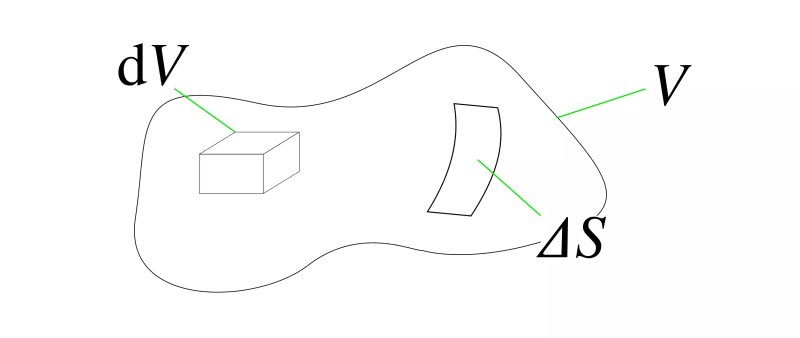
時刻$t$におけるこの連続体の体積、速度、密度をそれぞれ$V(t), v, \rho$とします。このとき、運動量の定義からこの連続体の持つ運動量$\{P\}$は次の通り表せます¹。 \begin{equation} \{P\} = \int_V \rho\{v\} dV \end{equation}

この領域$V$には物体力と表面力のみが作用しており、単位質量当たりに働く物体力$\{K\}$を考えると、$V(t)$全体に働く物体力は次の通り表せます¹。 \begin{equation} \int_V \rho\{K\} dV \end{equation}

同様に表面力についても考えます。この体積$V$の表面積$S$と微小面積$\Delta S$を用いると、この体積要素全体に作用する表面力は次の通り表せます¹。 \begin{equation} \int_S \{t\} dS \end{equation}

式(2)、(3)、(4)より、オイラーの第一運動法則と呼ばれる、連続体の運動方程式は次の通り表せます¹。 \begin{eqnarray} \frac{D}{Dt}\int_V \rho\{v\} dV = \int_V \rho\{K\} dV + \int_S \{t\} dS\nonumber\\[ 5pt ] \int_V \rho\{a\} dV = \int_V \rho\{K\} dV + \int_S \{t\} dS \end{eqnarray}

オイラーの第二運動法則

先ほどの微小体積の角運動量$\{H\}$は次式で表せます¹。なお、ここでのベクトルの乗算は外積を意味しています。 \begin{eqnarray} \{H\} &=& \{r\}\times\{P\} \nonumber\\[ 5pt ] &=& \int_V \rho \{r\}\times\{v\} dV \end{eqnarray}

これにより、式(5)を用いて連続体の角運動方程式は次式の通り表せます¹。 \begin{equation} \int_V \rho\{r\}\times\{a\} dV = \int_V \rho\{r\}\times\{K\} dV + \int_S \{r\}\times\{t\} dS \end{equation}

コーシーの運動方程式

コーシーの運動方程式はオイラーの第一運動法則と本質的には同じです。コーシーの運動方程式の特徴として、応力テンソルが用いられているという点と微分形で表されている点が挙げられます。

まずコーシーの応力公式は応力ベクトル$\{t\}$と応力テンソル$\left[\sigma\right]$および法線単位ベクトル$\{n\}$を用いて \begin{equation} \{t\} = \left[\sigma\right]\{n\} \end{equation} の通り表せ、これにガウスの発散定理を途中で適用して変形すると、 \begin{eqnarray} \int_S \{t\}dS &=& \int_S \left[\sigma\right]\{n\} dS \nonumber\\[ 5pt ] &=& \int_S \left[\sigma\right]\{dS\} \nonumber\\[ 5pt ] &=& \int_V \nabla\cdot\left[\sigma\right]dV \end{eqnarray} となります。式(9)を式(5)へ代入し変形します。 \begin{eqnarray} \int_V \rho\{a\} dV &=& \int_V \nabla\cdot\left[\sigma\right] dV + \int_V \rho \{K\} dV \nonumber\\[ 5pt ] &=& \int_V \bigl(\nabla\cdot\left[\sigma\right] + \rho \{K\} \bigr)dV \end{eqnarray} 結果として式(10)から次式のコーシーの運動方程式が得られます。 \begin{equation} \rho\{a\} = \nabla\cdot\left[\sigma\right]+ \rho \{K\} \end{equation}

平衡方程式

平衡方程式はコーシーの運動方程式から加速度の項を除いたものです。具体的には連続体に働く力が釣り合っている状態かつモーメントがつり合っている状態を表しています。

平衡方程式を表す方法は幾つかありますが、ここでは上述したコーシーの運動方程式から加速度の項を除いた場合を考えます。従って式は \begin{equation} \nabla\cdot\left[\sigma\right]+ \rho \{K\} = 0 \end{equation}

となります。

さいごに

次回、応力テンソルが対称テンソルとなることと、対象テンソルで表せる前提条件について解説します。

中村喜代次，森教安著，連続体力学の基礎，コロナ社(2012)，pp. 96 - pp. 97． ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎